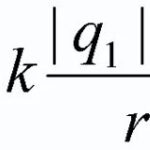Vládne Lorentzova sila a ľavá ruka. Pohyb nabitých častíc v magnetickom poli

Umiestnené v magnetickom poli vodičcez ktorý prešiel elektriny, je ovplyvnená silou Ampéra $F_A$ a jeho hodnotu možno vypočítať pomocou nasledujúceho vzorca:

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

kde $ja$ a $l$ - sila prúdu a dĺžka vodiča, $B$ - indukcia magnetického poľa, $\alpha$ - uhol medzi smermi sily prúdu a magnetickej indukcie. Prečo sa to deje?

Lorentzova sila. Pohyb nabitej častice v magnetickom poli.

Obsah

1 Čo je Lorentzova sila - určenie, kedy k nej dôjde, získanie vzorca
2 Určenie smeru Lorentzovej sily pomocou pravidla ľavej ruky
3 Pohyb nabitej častice v magnetickom poli
4 Aplikácia Lorentzovej sily v strojárstve

Čo je Lorentzova sila - určenie, kedy k nej dôjde, získanie vzorca

Je známe, že elektrický prúd je usporiadaný pohyb nabitých častíc. Zistilo sa tiež, že počas pohybu v magnetickom poli je každá z týchto častíc vystavená pôsobeniu sily. Aby sila vznikla, častica musí byť v pohybe.

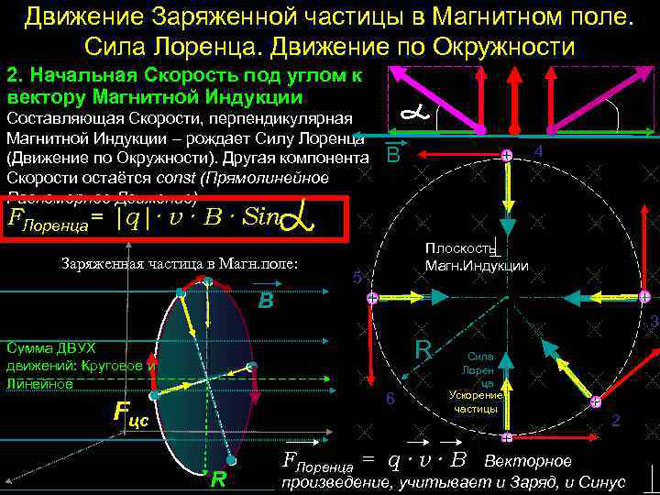
Lorentzova sila je sila, ktorá pôsobí na elektricky nabitú časticu, keď sa pohybuje v magnetickom poli.Jeho smer je kolmý na rovinu, v ktorej ležia vektory rýchlosti častíc a intenzity magnetického poľa. Výsledkom Lorentzových síl je sila Ampéra. Keď to vieme, môžeme odvodiť vzorec pre Lorentzovu silu.

Čas potrebný na to, aby častica prešla segmentom vodiča, $t = \frac {l}{v}$ , kde $l$ - dĺžka segmentu, $v$ je rýchlosť častice. Celkový náboj prenesený počas tejto doby cez prierez vodiča, $Q = I\cdot t$ . Nahradením časovej hodnoty z predchádzajúcej rovnice máme

$Q = \frac {I\cdot l}{v}$ (2)

V rovnakom čase $F_A=F_L\cdot N$ , kde $N$ je počet častíc v uvažovanom vodiči. V čom $N = \frac {Q}{q}$ , kde $q$ je náboj jednej častice. Nahradenie hodnoty do vzorca $Q$ z (2) možno získať:

$N = \frac {I\cdot l}{v\cdot q}$

Touto cestou,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

Pomocou (1) možno predchádzajúci výraz zapísať ako

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

Po kontrakciách a presunoch sa objaví vzorec na výpočet Lorentzovej sily

$F_L = q\cdot v\cdot B\cdot sin\alpha$

Vzhľadom na to, že vzorec je napísaný pre modul sily, musí byť napísaný takto:

Prečítajte si tiež: Ako previesť zosilňovače na watty a naopak?

$F_L = |q|\cdot v\cdot B\cdot sin\alpha$ (3)

Pretože $sin\alpha = sin(180^{\circ} - \alpha)$ , potom na výpočet Lorentzovho silového modulu nezáleží na tom, kam smeruje rýchlosť, - v smere sily prúdu alebo proti, - a môžeme povedať, že $\alpha$ je uhol, ktorý zvierajú vektory rýchlosti častíc a magnetickej indukcie.

Zápis vzorca vo vektorovej forme bude vyzerať takto:

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}]$

$[\vec{v}\times \vec{B}]$ je krížový súčin, ktorého výsledkom je vektor s modulom rovným $v\cdot B\cdot sin\alpha$ .

Na základe vzorca (3) môžeme konštatovať, že Lorentzova sila je maximálna v prípade kolmých smerov elektrického prúdu a magnetického poľa, to znamená, keď $\alpha = 90^{\circ}$ a zmiznú, keď sú rovnobežné ( $\alpha = 0^{\circ}$ ).

Je potrebné mať na pamäti, že na získanie správnej kvantitatívnej odpovede - napríklad pri riešení úloh - by sa mali používať jednotky sústavy SI, v ktorej sa magnetická indukcia meria v teslach (1 T = 1 kg s⁻²·ALE⁻¹), sila - v Newtonoch (1 N = 1 kg m/s²), sila prúdu - v ampéroch, náboj v coulombách (1 C = 1 A s), dĺžka - v metroch, rýchlosť - v m/s.

Určenie smeru Lorentzovej sily pomocou pravidla ľavej ruky

Keďže Lorentzova sila sa vo svete makroobjektov prejavuje ako Ampérova sila, na určenie jej smeru možno použiť pravidlo ľavej ruky.

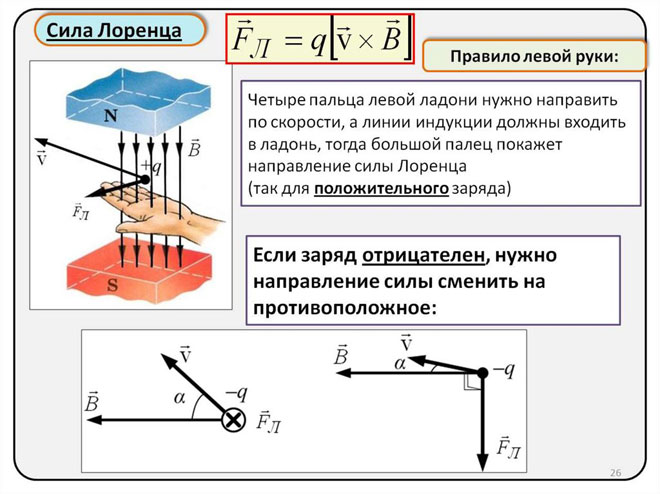
Určenie smeru pôsobenia Lorentzovej sily podľa pravidla ľavej ruky.

Ľavú ruku musíte položiť tak, aby bola otvorená dlaň kolmá na čiary magnetického poľa a smerom k nim, štyri prsty by mali byť natiahnuté v smere sily prúdu, potom bude Lorentzova sila smerovať tam, kde ukazuje palec, ktorý by mal byť ohnutý.

Pohyb nabitej častice v magnetickom poli

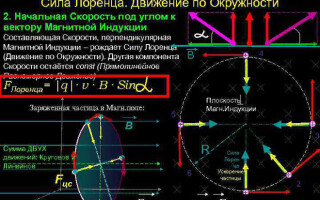
V najjednoduchšom prípade, to znamená, keď sú vektory magnetickej indukcie a rýchlosti častíc ortogonálne, Lorentzova sila, ktorá je kolmá na vektor rýchlosti, môže zmeniť iba svoj smer. Veľkosť rýchlosti a energie preto zostanú nezmenené. To znamená, že Lorentzova sila pôsobí analogicky s dostredivou silou v mechanike a častica sa pohybuje v kruhu.

Prečítajte si tiež: Koľko wattov je v kilowatte?

V súlade s Newtonovým zákonom II ( $F = m\cdot a$ ) môžeme určiť polomer rotácie častice:

$N = \frac {m\cdot v}{q\cdot B}$ .

Treba poznamenať, že so zmenou špecifického náboja častice ( $\frac {q}{m}$ ) sa mení aj polomer.

V tomto prípade je doba rotácie T = $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . Nezávisí od rýchlosti, čo znamená, že vzájomná poloha častíc s rôznou rýchlosťou bude nezmenená.

Pohyb nabitej častice v rovnomernom magnetickom poli.

V komplikovanejšom prípade, keď je uhol medzi rýchlosťou častice a intenzitou magnetického poľa ľubovoľný, bude sa pohybovať po špirálovej trajektórii - translačne v dôsledku zložky rýchlosti nasmerovanej rovnobežne s poľom a pozdĺž kruhu pod vplyvom jej kolmá zložka.

Aplikácia Lorentzovej sily v strojárstve

Kineskop

Kineskop, ktorý stál donedávna, keď bol nahradený LCD (plochou) obrazovkou, v každom televízore, nemohol fungovať bez Lorentzovej sily. Na vytvorenie televízneho rastra na obrazovke z úzkeho prúdu elektrónov sa používajú vychyľovacie cievky, v ktorých vzniká lineárne sa meniace magnetické pole. Horizontálne cievky pohybujú elektrónovým lúčom zľava doprava a vracajú ho späť, personálne cievky sú zodpovedné za vertikálny pohyb, pohybujúc lúčom prebiehajúcim horizontálne zhora nadol. Rovnaký princíp sa používa v osciloskopy - prístroje používané na štúdium striedavého elektrického napätia.

hmotnostný spektrograf

Hmotnostný spektrograf je zariadenie, ktoré využíva závislosť polomeru rotácie nabitej častice od jej špecifického náboja. Princíp jeho fungovania je nasledujúci:

Zdroj nabitých častíc, ktoré naberajú rýchlosť pomocou umelo vytvoreného elektrického poľa, je umiestnený vo vákuovej komore, aby sa vylúčil vplyv molekúl vzduchu. Častice vyletujú zo zdroja a po prechode pozdĺž oblúka kruhu zasiahnu fotografickú platňu a zanechajú na nej stopy. V závislosti od konkrétneho náboja sa mení polomer trajektórie a tým aj bod dopadu. Tento polomer sa dá ľahko zmerať a ak ho poznáte, môžete vypočítať hmotnosť častice. Pomocou hmotnostného spektrografu sa napríklad skúmalo zloženie mesačnej pôdy.

Prečítajte si tiež: Aké profesie súvisia s elektrinou

cyklotrón

Nezávislosť periódy, a teda aj frekvencie rotácie nabitej častice od jej rýchlosti v prítomnosti magnetického poľa, sa využíva v zariadení nazývanom cyklotrón a je určené na zrýchlenie častíc na vysoké rýchlosti. Cyklotrón sú dva duté kovové polvalce - dee (tvarom každý z nich pripomína latinské písmeno D) umiestnené rovnými stranami k sebe v krátkej vzdialenosti.

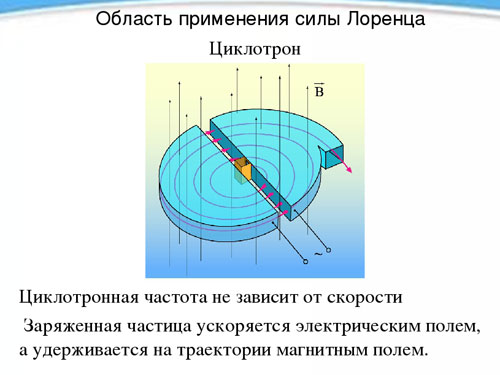
Cyklotrón - aplikácia Lorentzovej sily.

Dees sú umiestnené v konštantnom rovnomernom magnetickom poli a medzi nimi sa vytvára striedavé elektrické pole, ktorého frekvencia sa rovná frekvencii rotácie častice, ktorá je určená intenzitou magnetického poľa a špecifickým nábojom. Keď sa častica dostane dvakrát počas obdobia rotácie (počas prechodu z jedného dee do druhého) pod vplyvom elektrického poľa, zakaždým sa zrýchli, čím sa zväčší polomer trajektórie a v určitom okamihu, keď dosiahne požadovanú rýchlosť, vyletí zo zariadenia cez otvor. Týmto spôsobom môže byť protón urýchlený na energiu 20 MeV (megaelektrónvolt).

Magnetron

Zariadenie nazývané magnetrón, ktoré je inštalované v každom mikrovlnka, je ďalším zástupcom zariadení využívajúcich Lorentzovu silu. Magnetrón slúži na vytvorenie výkonného mikrovlnného poľa, ktoré ohrieva vnútorný objem rúry, kde je umiestnený pokrm. Magnety zahrnuté v jeho zložení korigujú trajektóriu pohybu elektrónov vo vnútri zariadenia.

Magnetické pole Zeme

A v prírode hrá Lorentzova sila pre ľudstvo mimoriadne dôležitú úlohu. Jeho prítomnosť umožňuje magnetickému poľu Zeme chrániť ľudí pred smrteľným ionizujúcim žiarením vesmíru. Pole neumožňuje nabitým časticiam bombardovať povrch planéty, čo ich núti zmeniť smer.

Podobné články: